LIMITES
1°) Définition.
Soit une fonction f(x) définie sur D un intervalle de R.
On dit que f(x) tend vers une limite l quand x tend vers x0
Î D, si :
"
e
> 0 $
a
> 0 "
x ¹
x0 tel que | x- x0 | < a
alors | f(x) -
l
| < e .
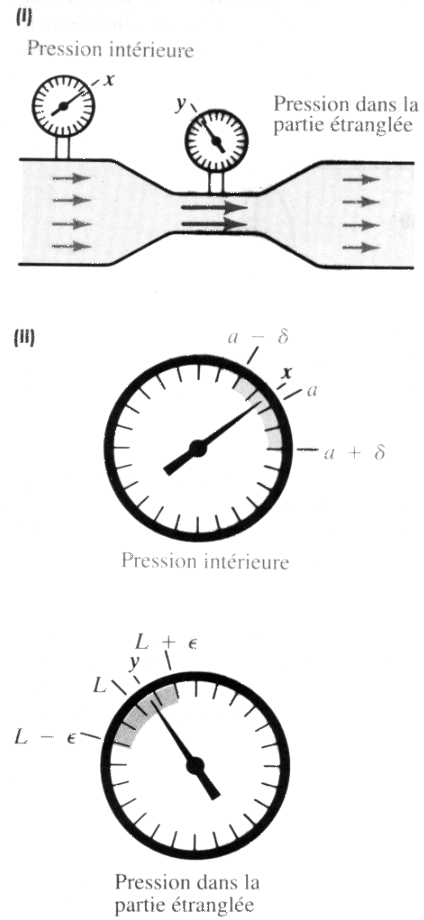
Exemple 1:
Un fluide s’écoule de gauche à droite, on voudrait que la
pression y dans la partie étranglée soit toujours comprise dans
l’encadrement
l -
e
< y < l
+ e
, ce qui est équivalent à
| y -
l
| < e.
Il faut donc que la pression dans la première partie soit elle aussi
comprise dans un certain encadrement
x0 - a
< x < x0 + a
, ce qui est équivalent à
| x - x0 | < a
.
Le problème revient donc à la recherche d’un
a
en fonction d’un e
donné.
Exemple 2:
Montrer que 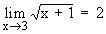 .
.
On cherche a tel que | x- 3 | <
a Þ |
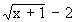 | <
e
| <
e
| 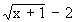 | =
| =
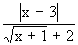 <
<
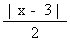
de sorte que si | x- 3 | < 2.e
alors | 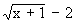 | <
e.
| <
e.
Il suffit de prendre a
= 2.e
.
De même:
On dit que f(x) a une limite
l
quand x tend vers +¥
, si:
"
e
> 0 $
A > 0 "
x Î
R tel que x > A alors | f(x) -
l
| < e
.
Exemple:
On dit que f(x) a une limite
l
quand x tend vers -¥
, si:
"
e
> 0 $
A > 0 "
x ¹
x0 tel que x < -A alors | f(x) -
l | < e .
On dit que f(x) tend vers +¥
quand x tend vers x0 , si:
"
A > 0 $
a
> 0 "
x ¹
x0 tel que | x- x0 | < a
alors f(x) > A.
On dit que f(x) tend vers -¥
quand x tend vers x0 , si:
"
A > 0 $
a
> 0 "
x ¹
x0 tel que | x- x0 | < a
alors f(x) < -A.
2°) Limite à droite, Limite à gauche.
Exemple: Soit la fonction f (x) = 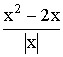 définie sur R*.
définie sur R*.
Si x>0 alors f (x) = x - 2 et la limite de f(x) quand x tend vers 0 vaut (-2).
Si x<0 alors f (x) = -x + 2 et la limite de f(x) quand x tend vers 0 vaut (+2).
-
On dit que la fonction f admet une limite en x0 si
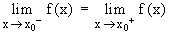 .
.
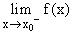 se lit " limite à gauche en x0 ",
se lit " limite à gauche en x0 ",
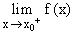 se lit " limite à droite en x0 ".
se lit " limite à droite en x0 ".
3°) Opérations sur les limites:
La recherche des limites est facilitée par les
théorèmes suivants:
- La limite d’une somme de fonctions est égale à la somme des limites
de ces fonctions.
- La limite d’un produit de fonctions est égale au produit des limites de
ces fonctions.
- La limite d’un quotient de fonctions est égale au quotient des limites
de ces fonctions, sous réserve que la limite du dénominateur ne
soit pas nulle.
- Si g(x) < f(x) < h(x) et
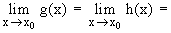
l alors
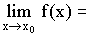 l.
l.
Exemple: 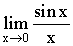 ?
?
- La limite d’un polynôme en ¥
est la limite de son terme de plus haut degré.
Soit le polynôme P(x) = 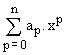 = an.xn + ... + a1
.x1 + a0.
= an.xn + ... + a1
.x1 + a0.
P(x) =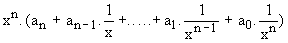
or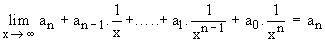
d’où 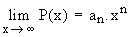
- La limite d’une fonction rationnelle en ¥
est la limite du quotient des termes de plus haut degré du
numérateur et du dénominateur.
Exemple: Calculer
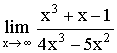 .
.
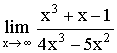 =
=
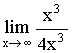 =
=
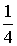 .
.
4°) Formes indéterminées.
Dans certains cas, les théorèmes précédents,
relatifs à la limite d’une somme, d’un produit, d’un quotient ou autre
ne permettent pas de conclure; l’expression considérée se
présente alors sous une forme dite " forme
indéterminée ". Ces formes sont:
" ¥
- ¥
" , " 0 ´
¥
" , " ¥
/ ¥
" , " 0 / 0 " . Nous verrons dans les chapitres
suivants qu’il existe d’autres formes indéterminées comme:
" 1¥
" , " 00 " et "
¥
0 " .
On dit qu’on a levé l’indétermination lorsque l’on a
trouvé la limite.
5°) Etude des branches infinies.
CONTINUITE
1°) Continuité en un point.
Une fonction f(x), définie au voisinage de x0 , est dite
continue en x0 si 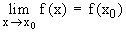 ou encore "
e > 0 $
n > 0 | x- x0 | < n Þ
| f(x) - l | < e .
ou encore "
e > 0 $
n > 0 | x- x0 | < n Þ
| f(x) - l | < e .
2°) Cas de discontinuité en un point.
3°) Continuité sur un segment.
Soit [a , b] un segment sur lequel la fonction f est définie.
Elle sera continue sur [a , b] si:
- Elle est continue en tout point de l’ouvert ] a , b [.
- Elle est continue à droite de a et continue à gauche de b.
Théorèmes:
- Toute fonction continue sur [a , b] est bornée c’est à dire
m est la borne inférieure est notée m =
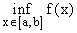 .
.
M est la borne inférieure est notée M =
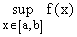 .
.
- Toute fonction continue sur [ a , b ] prend au moins toute valeur
mm comprise entre m et M.
Corollaire:
Une fonction ne peut changer de signe qu’en s’annulant ou en cessant d’être
continue et si f(a) et f(b) sont de signes contraires, l’équation f(x)= 0 admet
au moins une solution dans [ a , b].
Ce résultat est utilisé pour résoudre numériquement une
équation.
- Une fonction f est continue par morceaux sur un intervalle D si elle admet en chaque
point de D une limite à gauche et une limite à droite.
4°) Opération sur les fonctions continues
Nous admettrons sans démonstration les théorèmes suivants:
- Si f et g sont des fonctions continues, alors f + g est une fonction continue.
- Si f est continue en x0, l
f est continue en x0, l
Î
R.
- Si f et g sont continue en x0, f´
g est continue en x0, ainsi que f/g si g(x0).
- Si f est continue en x0 et positive au voisinage de x0
,
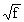 est continue en x
0.
est continue en x
0.
- Si f est continue en x0 et g en y0 = f(x0)
la fonction composée h = g o f est continue en x0.

![]() .
.![]() | <
e
| <
e![]() | =
| =
![]() <
<
![]()
![]() | <
e.
| <
e.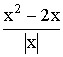 définie sur R*.
définie sur R*.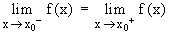 .
.![]() se lit " limite à gauche en x0 ",
se lit " limite à gauche en x0 ",
![]() se lit " limite à droite en x0 ".
se lit " limite à droite en x0 ".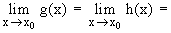
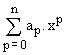 = an.xn + ... + a1
.x1 + a0.
= an.xn + ... + a1
.x1 + a0.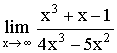 .
.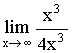 =
=